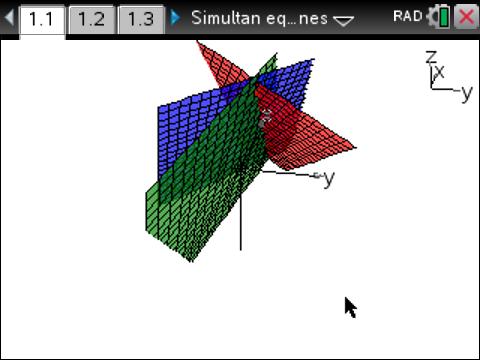
You can solve a system of three simultaneous equations using matrices and visualize the solutions in a 3D graph on a TI-Nspire CAS calculator. This allows for a clear and geometric representation of the solution in three-dimensional space.
$0.00
Graphing the intersection of planes using matrices in a 3D graph on a TI-Nspire CAS calculator can be a powerful tool for visualizing and understanding systems of linear equations in three variables. By following shown steps, you can graphically visualize the intersection of planes using matrices in a 3D graph on a TI-Nspire CAS calculator, which can be especially useful when dealing with systems of linear equations in three variables.
Unique Solution:
When the number of equations is equal to the number of variables (n equations with n variables) and the system is consistent (i.e., equations are not contradictory), a unique solution exists.
No Solution: When the number of equations is less than the number of variables (n equations with m < n variables), the system may have no solution.
When, after performing row operations, a contradictory equation such as “0 = a nonzero constant” appears in the system, it has no solution.
When two parallel planes in three-dimensional space are being described by the equations and they do not intersect, the system has no solution.
Infinite Number of Solutions: When the number of equations is less than the number of variables (n equations with m > n variables), and the equations are dependent (one can be expressed as a linear combination of others), an infinite number of solutions exist.
When, after performing row operations, some equations become identical or proportional to each other, the system has an infinite number of solutions.
In cases where a plane intersects another plane along a line, the system of equations describing these planes will have an infinite number of solutions.