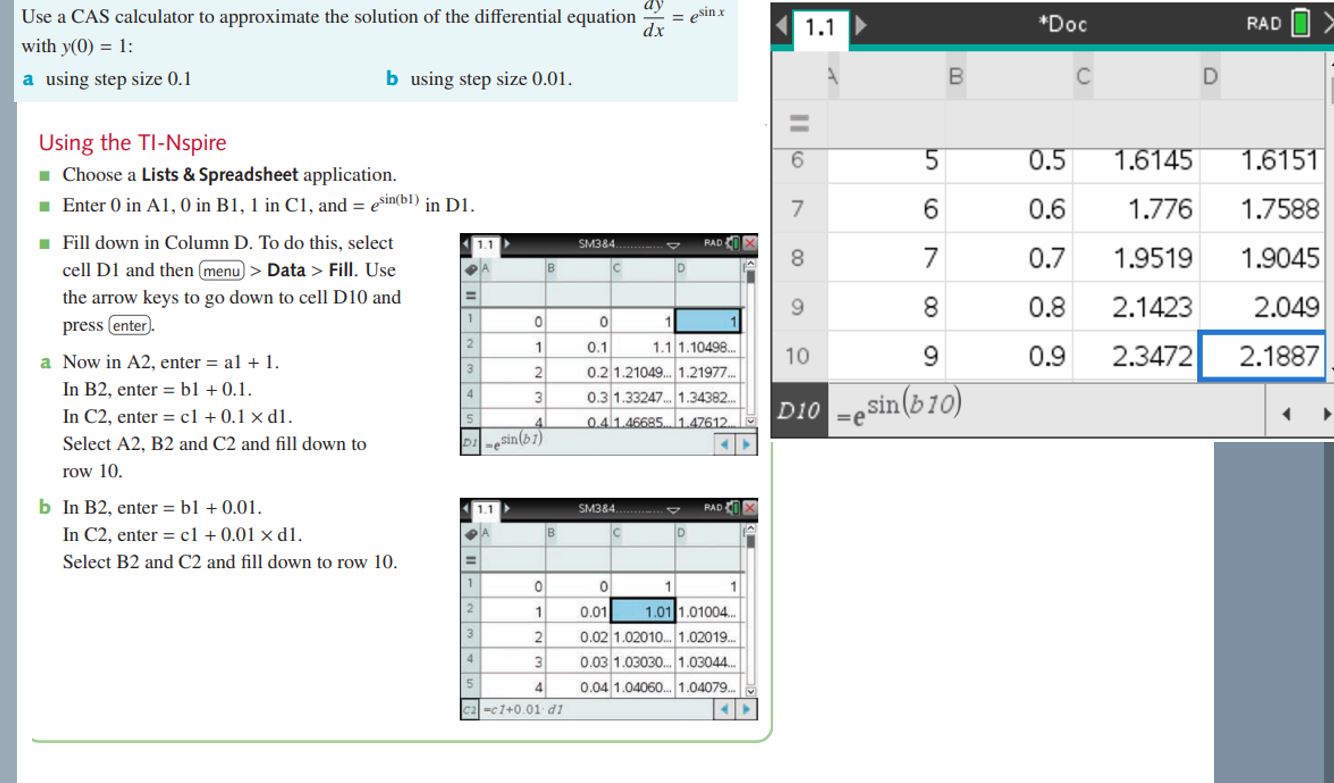
In the realm of numerical analysis, Euler’s method stands as a fundamental tool for approximating solutions to differential equations. This approach is particularly useful when exact solutions are challenging to obtain. The basic idea behind Euler’s method is to break down a continuous problem into smaller steps, allowing for a step-by-step approximation.

Using Euler’s method to solve numerically a differential equation. Theory, example, past exam questions. To facilitate the numerical calculations involved in Euler’s method, modern tools like TI-Nspire calculators offer spreadsheet functionalities. You can set up a spreadsheet to automate the iterative process, making it more efficient and less prone to errors.