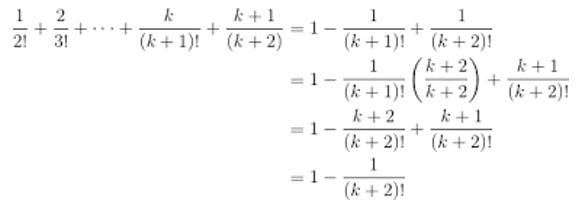• Direct proof
• Proof by contradiction
• Proof by counter examples
• Proof by mathematical induction
• Proof by contrapositive
  These methods form the foundation of mathematical reasoning and are used to establish the validity of mathematical statements rigorously. Each method has its own strengths and is chosen based on the nature of the problem at hand.

For mathematicians, a proof is an argument that leaves no room for doubt.
Each step in a proof is based on axioms, which are fundamental truths accepted without proof.
The statements derived from these axioms are known as theorems.
In mathematics, a conjecture is a statement that appears to be true but has not yet been formally proven. It represents a mathematician’s belief or educated guess about a pattern or relationship, awaiting verification through rigorous proof.