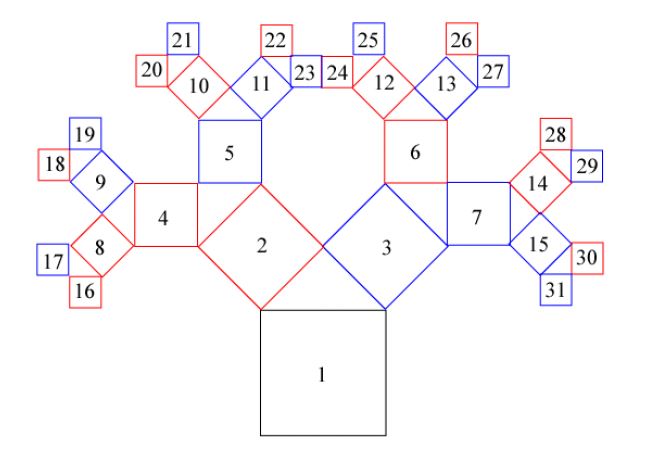
Pythagorean tree with matrices, transformations and binary numbers.
$0.00
A Pythagorean tree is generated by taking a square and adding 2 smaller squares that have been rotated and dilated so a right-angle triangle is formed. The hypotenuse of the right-angled triangle is the length of the original square and the other legs of the triangle are the lengths of the added squares. By continuing this with each successive square created, we can create the Pythagorean tree fractal. For example, here are the first few iterations when the added squares have equal lengths: (when we create an isosceles right triangle between the 3 squares and the two added squares are congruent). For this investigation, we will focus only on Pythagorean tree fractals created with equally sized squares at each stage so that isosceles right-angled triangles are created in between the squares. the use of TI Nspire CAS is incorporated in the investigation. The extension includes walks with binary numbers.