In this Year 10 mathematics variation activity, students will investigate the concepts of direct variation and inverse variation using two different scenarios: triangular numbers and light intensity.
$0.00
Direct Variation with Triangular Numbers:
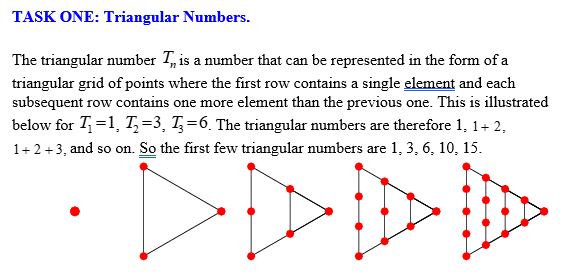
- Define triangular numbers as a sequence of numbers that can be represented as dots arranged in equilateral triangles. For example, the first triangular number is 1, the second is 3, the third is 6, and so on.
- Show students how the nth triangular number, T(n), can be calculated using the formula: T(n) = (n * (n + 1)) / 2.
- Explain that in the context of triangular numbers, the relationship between n and T(n) is a direct variation. As n increases, T(n) increases proportionally.
Activity:
- Provide students with a worksheet or a list of n-values and ask them to calculate the corresponding T(n) values.
- Have students graph their results on a coordinate plane with n on the x-axis and T(n) on the y-axis. Discuss how the graph represents direct variation and determine the constant of variation (k) from their graphs.
Part 2: Inverse Variation – Light Intensity
Introduction: Introduce the concept of inverse variation. Explain that in inverse variation, one variable increases as the other decreases, and it can be represented by an equation of the form y = k/x.
Inverse Variation with Light Intensity:
- Discuss light intensity as an example of inverse variation. Explain that as you move away from a light source, the intensity of light decreases inversely proportional to the square of the distance.
- Present the formula for inverse variation: I ∝ 1/d^2, where I represents light intensity, and d represents the distance from the light source.
Activity:
- Provide students with data on light intensity and distance from a light source. Ask them to calculate and graph the relationship between light intensity (I) and distance (d).
- Discuss how the graph represents inverse variation, and encourage students to identify the constant of variation (k) from their graphs.
Conclusion:
Wrap up the activity by summarizing the key concepts of direct and inverse variation, emphasizing their relevance in real-world scenarios like triangular numbers and light intensity. Discuss how these mathematical concepts are applied in various fields.
This activity engages students in exploring direct and inverse variation through both theoretical and practical applications, helping them grasp these mathematical concepts and their real-world significance.